Blog Archive
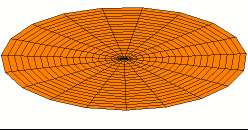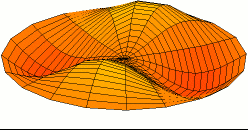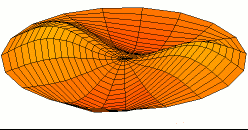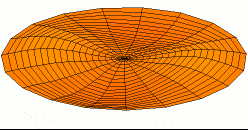
Salah satu mode getaran gendang
Jenis getaran
Getaran bebas terjadi bila sistem mekanis dimulai dengan gaya awal, lalu dibiarkan bergetar secara bebas. Contoh getaran seperti ini adalah memukul garpu tala dan membiarkannya bergetar, atau bandul yang ditarik dari keadaan setimbang lalu dilepaskan.Getaran paksa terjadi bila gaya bolak-balik atau gerakan diterapkan pada sistem mekanis. Contohnya adalah getaran gedung pada saat gempa bumi.
Analisis getaran
Dasar analisis getaran dapat dipahami dengan mempelajari model sederhana massa-pegas-peredam kejut. Struktur rumit seperti badan mobil dapat dimodelkan sebagai "jumlahan" model massa-pegas-peredam kejut tersebut. Model ini adalah contoh osilator harmonik sederhana.Getaran bebas tanpa peredam
Pada model yang paling sederhana redaman dianggap dapat diabaikan, dan tidak ada gaya luar yang mempengaruhi massa (getaran bebas).Dalam keadaan ini gaya yang berlaku pada pegas Fs sebanding dengan panjang peregangan x, sesuai dengan hukum Hooke, atau bila dirumuskan secara matematis:
Sesuai Hukum kedua Newton gaya yang ditimbulkan sebanding dengan percepatan massa:
Bila massa dan kekakuan (tetapan k) diketahui frekuensi getaran sistem akan dapat ditentukan menggunakan rumus di atas.
[sunting] Getaran bebas dengan redaman
Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluida benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) c ini dinamakan koefisien peredam, dengan satuan N s/m (SI)Nilai koefisien redaman yang diperlukan untuk mencapai titik redaman kritis pada model massa-pegas-peredam adalah:
Solusi sistem kurang redam pada model massa-pegas-peredam adalah
Nilai X, amplitudo awal, dan φ, ingsutan fase, ditentukan oleh panjang regangan pegas.
Dari solusi tersebut perlu diperhatikan dua hal: faktor eksponensial dan fungsi cosinus. Faktor eksponensial menentukan seberapa cepat sistem teredam: semakin besar nisbah redaman, semakin cepat sistem teredam ke titik nol. Fungsi kosinus melambangkan osilasi sistem, namun frekuensi osilasi berbeda daripada kasus tidak teredam.
Frekuensi dalam hal ini disebut "frekuensi alamiah teredam", fd, dan terhubung dengan frekuensi alamiah takredam lewat rumus berikut.

Label
- Alkitab (5)
- anime (14)
- Arti nama (3)
- Automotif (138)
- Award (1)
- Bahaya (1)
- Bangunan Unik (8)
- belajar html (1)
- benda (24)
- Binatang (36)
- Biografi (81)
- Biologi (6)
- buah (12)
- cara belajar (2)
- CIA (1)
- Community (2)
- contact (1)
- Daerah (18)
- Dewa (2)
- Dijual (1)
- Download software (5)
- drift (1)
- Ekonomi (1)
- FBI (1)
- film (33)
- Fisika (11)
- Game (37)
- ganti kusor blog (1)
- Geografi (27)
- hacker (7)
- Hewan Punah (5)
- Ilmu (48)
- ilmu Beladiri (4)
- Istilah (5)
- kata kata bijak (2)
- kata2 bijak (1)
- Kecepatan (14)
- kimia (1)
- kisah nyata (6)
- Komputer (7)
- Kristen (4)
- kuno (6)
- LAPD (1)
- link (2)
- lirik lagu (3)
- membuat virus (1)
- membuat virus melalui notepad (1)
- membuat virus via notepad (1)
- Misteri (67)
- Misteri dunia (51)
- Mitos (10)
- NASA (88)
- negara (5)
- Organisasi (2)
- Parkour (1)
- Pelajaran (1)
- Perjalanan (1)
- Perkembangan (2)
- petshop (9)
- petugas (1)
- PKN (3)
- pohon (5)
- Puisi (1)
- pulau (9)
- Rahasia (1)
- rubic (2)
- Saion (1)
- sastra (3)
- sejarah (29)
- Senjata (73)
- situs populer (7)
- Sniper (1)
- tata surya (27)
- Teknik (15)
- telepati (1)
- Tenga dalam (1)
- the power of kepepet (1)
- The Three Kingdom (8)
- TIps Binatang (10)
- Tips blogger (4)
- tradisi (9)
- tragedi (4)
- trick magic (2)
- Tumbuhan (1)
- UFO (1)
- Yesus (2)
Loading
Tian's Fan Box
Tian on Facebook
Copyright 2010 Tian
Theme designed by Lorelei Web Design
Blogger Templates by Blogger Template Place | supported by One-4-All




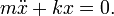

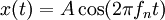
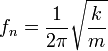

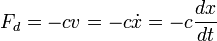


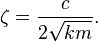






0 komentar:
Posting Komentar